Archive for the ‘Algorithm’ Category
Code Challenge by the Trustpilot Development Team
On the news
I heard Trustpilot got a huge funding.
I stumbled on their website to get some Idea what kind of company they were and to get some inspiration of how they build their website.
Then I saw they were looking for new developers and decided to see what they were looking for to get an idea of how the company operate, the tech behind the company.
They have an anagram puzzle which must be solved in order to apply for a job.
Wow, that is a very interesting concept.
Disclaimer
I will not give any spoiler, the secret phrase will not be given.
Code challenge
A programming task to test that the candidate is able to fit the job description.
The designed the assignment webpage in the Matrix movie theme.
They also have one for a frontend developer
http://followthewhiterabbit.trustpilot.com/fe/index.html
That challenge is quickly solved if you know some frontend, but in the end, they want you to create a Trustpilot widget (html component) and submit that along with your resume.
Great concept. They want to test that you can solve a realistic assignment before you are called in for an interview.
This one is for a backend developer.
http://followthewhiterabbit.trustpilot.com/cs/step3.html
You’ve made an important decision. Now, let’s get to the matter.
We have a message for you. But we hid it.
Unless you know the secret phrase, it will remain hidden.Can you write the algorithm to find it?
Here is a couple of important hints to help you out:
– An anagram of the phrase is: “poultry outwits ants”
– The MD5 hash of the secret phrase is “4624d200580677270a54ccff86b9610e”
Here is a list of english words, it should help you out.Type the secret phrase here to see if you found the right one
Trustpilot Development Team
The list of English words contains 99175 words.
When you type in the secret phase, the phase is translated to a SHA256 hash key which forms a part of the url which contains information of how to apply.
Ok I get it. Hash is for verification. I cannot derive the anagram words out of the MD5 hash value.
The SHA256 hash function generates a cryptic hash value, which forms part of a url. That means I cannot guess the url result.
Anagram puzzle illustrated with Legos
The Lego pieces represent the letters. The way the Lego’s are arranged represent the words.
This Lego (poultry outwits ants)

Is an anagram of this Lego (the sentence we are searching for)

Because they have the same amount of piece types and colors

This represents a part of the sentence, an English word from the list

This represents a part of the sentence, an English word from the list

This represents a part of the sentence, an English word from the list

They form the phrase we are looking for when taken together and arranged in a specific way.

We can build Lego buildings by combining items from the list.
We know we have found the correct Lego building (secret phrase) when the MD5 function gives the provided value.
Easy solution?
This puzzle made me curious and I wanted to see if there was a ‘quick win’.
By looking at the phrase “poultry outwits ants” I get a feeling there is trustpilot word in there.
After subtracting trustpilot I got left “y ouw ants”. Yah the phrase must be “trustpilot wants you”
I type that in and expected the ‘quick win’.
To my surprise I get this page.
Yes! That is indeed an anagram of the text, you got the drift.
But you were just guessing. It is not the magic phrase.
There is no way around it. Create an algorithm to solve it for real!
Go back, and try again!
Huh?! They expected I would guess that. Cool, respect to the Trustpilot dev team to create such a puzzle that anticipated my move.
All right, well played Trustpilot dev team, well played. Game on, I take the challenge, I want to solve this.
I tried other moves to get my ‘quick win’.
I typed 4624d200580677270a54ccff86b9610e.html as part of the url which is MD5 hash which I hoped would be same as the expected url but got.
Nope 🙂
In hindsight, kinda weak try by me because SHA256 and MD5 don’t produce the same result.
They were also looking for a frontend developer and had a task which I solved and noticed it had /fe/ as part of the solution url.
I tried to substitute the url with /be/ but alas I got.
Nope 🙂
I tried to lookup the MD5 hash on md5 cracker online but no luck, no result.
Ok no quick win for me.
I have to solve this the ‘correct’ way if I want to see the result page.
This is a well-designed and fun programming challenge with the Matrix theme.
It is clearly that they have put some time and effort in building these coding challenges.
Text animations, well-thought concept, fonts and colors.
Kudos to the Trustpilot dev team.
Analysis
"poultry outwits ants"
and
"trustpilot wants you"
Have three words.
And with the two spaces in the anagram I suspect it must be 3 words from the english word list.
I sure hope so, else I suspect that this could be a subset sum problem.
If it could be any 1 to N words from the list which satisfies the anagram condition then I suspect that would be a NP-complete problem and game over for me.
Not feasible for me to solve with my knowledge and with given dataset.
Not likely to be the case as it would be like to give a challenge which is impossible to solve.
Like this XKCD 🙂 http://xkcd.com/287/
The way it is phrased in the assignment and by the anagram example suggest that it is three words from the English list in a specific order.
Goal
So the goal is clear. Find 3 words from the list in a specific order which gives the MD5 hash value "4624d200580677270a54ccff86b9610e".
Brute forcing the list with ~ 100.000 words is not feasible in a reasonable time.
Strategy
Minimize the list and filter words out which cannot be part of the solution, then when the list is small enough, do brute force for a solution.
One of the ways to test whether a is an anagram of a' is to sort and compare them.
When the list is small enough, we take three words from the list, combine the words and sort them.
Taking all possible 3 words from a list has the running time O(n^3) where n is the list length.
That means with the strategy the list must be reduced from the ~100.000 items to about in few thousands at most to get a running time within few minutes at most.
If the sorted value is the same as the sorted anagram solution, we have a 3-word candidate for a solution.
The 3-word are arranged in the possible 6-ways they can be combined and a MD5 hash is calculated. If the calculated hash value is "4624d200580677270a54ccff86b9610e", then we have found the 3-word sentence we were looking for.
Result
After coding for a while, I managed to filter and reduce the list to 1659 items.
I did the brute forcing and one matching candidate appeared after the algorithm completed in about 1 minute.
I typed in the solution.
The page navigated me to the congratulations page.
Congratulations! You found the secret phrase. Are you the One?! 😉
You’re curious and you’re up for a challenge! So we like you already.
…
Well, that was fun. Thanks for fun puzzles Trustpilot 🙂
Get best k items from n items as fast as possible
SortedList2 – data structure example using C#
Reference: Selection algorithm
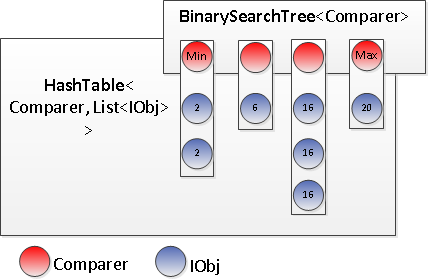
Recently I needed something like a SortedSet or SortedDictionary which supports multiple identical values.
I Explored the BCL but could not found the data structure I needed.
The scenarie:
I have a dataset size n where I want the k best items.
This is an alternative approach than using the selection algorithm.
Using selection algorithm is also much faster than the naive approach.
I will use Big O notations (beginners guide).
A sorted data structure should have the following operations (Binary search tree):
Insert(item) -> O(log n)
Exists(item) -> O(log n)
Remove(item) -> O(log n)
Max -> O(1)
Min -> O(1)
Count -> O(1)
Neither SortedList, SortedSet or SortedDictionary supports identical values and the listed operations.
The C5 collections has the TreeBag data structure and can be used for value types.
Naive version
Sort the data and take the k best items.
The worst case is O(n * log n).
The fastest optimistic running time will be Ω(n) (if the dataset is already sorted).
What if the we have the best k items on k iterations?
Inserting the first k items takes O(k * log k)
Checking for max item takes O(1).
For the n – k iteration: checking if there exists a better item takes O( (n - k) * log (1) )
On best case scenario this gives: Ω(k * log k + (n - k) * log (1)).
For k << n
that is Ω(n).
On average case for random distributed data where k << n the running time is:
Ω(n * log k).
I will implement a data structure SortedList2 which supports multiple identical comparable values
and test the running vs. a naive implementation.
I will use the SortedSet and the Dictionary structure.
The best item in this example is defined as: smallest even number.
Test cases
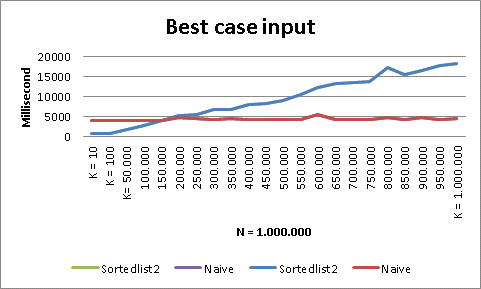
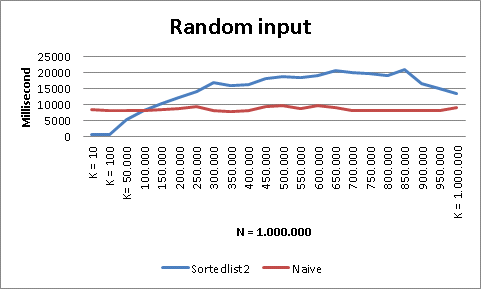
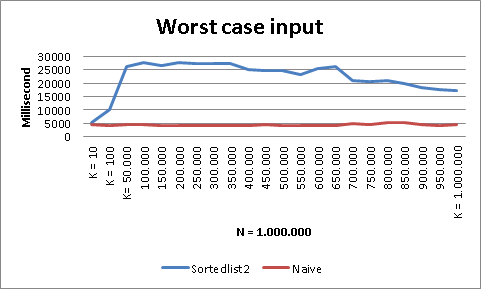
The result shows how the Sortelist2 performs for various k values versus the naive version.
To avoid the worst case input you can run the data through a randomizer filter which takes O(n).
Then the running time would be similar to the random input (It’s implemented in the attached source code).
When k < 10% of n then Sortedlist2 performs better.
n = 1.000.000
k = 5
Data distribution: best case
SortedList2 Elapsed: 556 msec. UId: 003 Comparer: 0 Name: n0 UId: 001 Comparer: 2 Name: duplicate UId: 002 Comparer: 2 Name: duplicate UId: 004 Comparer: 2 Name: n1 UId: 005 Comparer: 4 Name: n2 Naive Elapsed: 2707 msec. UId: 003 Comparer: 0 Name: n0 UId: 001 Comparer: 2 Name: duplicate UId: 002 Comparer: 2 Name: duplicate UId: 004 Comparer: 2 Name: n1 UId: 005 Comparer: 4 Name: n2
I assume the Naive version runs fast because the data is already sorted (compiler branch prediction).
The OrderBy runs faster than O(n * log n)
Data distribution: random
SortedList2 Elapsed: 523 msec. UId: 001 Comparer: 2 Name: duplicate UId: 002 Comparer: 2 Name: duplicate UId: 773997 Comparer: 2 Name: n773994 UId: 142607 Comparer: 6 Name: n142604 UId: 757235 Comparer: 6 Name: n757232 Naive Elapsed: 8483 msec. UId: 001 Comparer: 2 Name: duplicate UId: 002 Comparer: 2 Name: duplicate UId: 773997 Comparer: 2 Name: n773994 UId: 142607 Comparer: 6 Name: n142604 UId: 757235 Comparer: 6 Name: n757232
I ran this multiple times and the result were similar.
The Naive version runs clearly slow here.
Data distribution: worst case
SortedList2 Elapsed: 3269 msec. UId: 001 Comparer: 2 Name: duplicate UId: 002 Comparer: 2 Name: duplicate UId: 1000002 Comparer: 2 Name: n999999 UId: 1000001 Comparer: 4 Name: n999998 UId: 1000000 Comparer: 6 Name: n999997 Naive Elapsed: 2967 msec. UId: 001 Comparer: 2 Name: duplicate UId: 002 Comparer: 2 Name: duplicate UId: 1000002 Comparer: 2 Name: n999999 UId: 1000001 Comparer: 4 Name: n999998 UId: 1000000 Comparer: 6 Name: n999997
Here the Naive version is best for worst case input.
I assume the Naive version runs fast because the data is reverse sorted.
The OrderBy runs faster than O(n * log n)
n = 1.000.000
k = 100.000
Data distribution: best case
SortedList2 Elapsed: 1768 msec. Naive Elapsed: 2675 msec.
Data distribution: random
SortedList2 Elapsed: 6364 msec. Naive Elapsed: 6064 msec.
Data distribution: worst case
SortedList2 Elapsed:16478 msec. Naive Elapsed: 2590 msec.
Conclusion
If you want something fast for k << n then the Sortedlist2 (or the selection algorithms) are a better option than the naive approach.
Source code
Program.cs
using System;
using System.Collections.Generic;
using System.Diagnostics;
using System.Globalization;
using System.Linq;
using System.Threading;
namespace Datastructure
{
public class Program
{
static readonly Action<object> CW = Console.WriteLine;
const int MaxSize = 5;
const int N = 2 * 100 * 1000;
public static void Main(string[] args)
{
Thread.CurrentThread.CurrentCulture = CultureInfo.GetCultureInfo("en-US");
var stopwatch = new Stopwatch();
stopwatch.Start();
Run();
stopwatch.Stop();
CWF("\nSec: {0}\nPress a key to exit", stopwatch.Elapsed.ToString());
Console.ReadKey();
}
static void CWF(string s, params object[] a)
{
Console.WriteLine(s, a);
}
static void Run()
{
var comparer = new ObjComparer<Comparer>();
var rand = new Random();
var datas = new List<IObj>();
for (var i = 0; i < N; i++)
{
//datas.Add(new Obj { Comparer = new Comparer(i * 2), Name = "n" + i }); // best case
datas.Add(new Obj { Comparer = new Comparer(rand.Next(1, N)), Name = "n" + i }); // random
//datas.Add(new Obj { Comparer = new Comparer((N - i) * 2), Name = "n" + i }); // worst case
}
const bool displayList = true;
// --- Run sortedlist2
var sw = new Stopwatch();
sw.Start();
var sorted = new SortedList2(comparer);
//sorted.AddAll(datas, MaxSize, false); // method 1
foreach (var i in datas) sorted.Add(i, MaxSize); // method 2
var result = sorted.GetAll();
sw.Stop();
CWF("SortedList2 Elapsed: {0} msec.", sw.ElapsedMilliseconds);
if (displayList) foreach (var i in result) CW(i);
// --- Run naive
sw = new Stopwatch();
sw.Start();
datas.Sort(ObjComparer<IObj>.DoCompare);
result = datas.Take(MaxSize).ToList(); // method 1
//result = datas.OrderBy(i => i.Comparer).Take(MaxSize).ToList(); // method 2
sw.Stop();
CWF("\nNaive Elapsed: {0} msec.", sw.ElapsedMilliseconds);
if (displayList) foreach (var i in result) CW(i);
// --- Run selection algo
sw = new Stopwatch();
sw.Start();
var s = new Selection { List = datas, K = MaxSize };
s.Algo();
result = s.GetAll();
sw.Stop();
CWF("\nSelection algo Elapsed: {0} msec.", sw.ElapsedMilliseconds);
if (displayList) foreach (var i in result) CW(i);
}
}
public class Comparer : IComparable
{
public Comparer(int i) { Value = i; }
public long Value { get; set; }
public override int GetHashCode() { return this.Value.GetHashCode(); }
public override bool Equals(object obj)
{
var other = obj as Comparer;
if (other == null) return false;
var eq = this.GetHashCode().Equals(other.GetHashCode());
return eq;
}
public override string ToString()
{
return string.Format("{0}", Value.ToString());
}
/// <summary>
/// Comparison algo is implemented here
///
/// Even is best
/// If both or none are even then smallest is best
/// </summary>
/// <param name="obj"></param>
/// <returns></returns>
public int CompareTo(object obj)
{
var other = obj as Comparer;
if (other == null) return -1;
var a = (this.Value & 1) == 0; // is even?
var b = (other.Value & 1) == 0; // is even?
if (a && !b) return -1; // this is even, other is not
if (!a && b) return 1; // this is not even, other is
return this.Value.CompareTo(other.Value);
}
}
public class Obj : AObj, IObj
{
// Insert your custom properties here
public string Name { get; set; }
public override string ToString()
{
return string.Format("UId: {0:000} \t\tComparer: {1} \t\tName: {2}",
Uid, Comparer, Name);
}
public override int GetHashCode()
{
return Comparer.GetHashCode();
}
public override bool Equals(object obj)
{
var other = obj as IObj;
return other != null && this.GetHashCode().Equals(other.GetHashCode());
}
}
public interface IObj : IComparable
{
string Name { get; set; }
Comparer Comparer { get; set; }
}
public abstract class AObj : IComparable
{
private static int _counter;
public virtual int Uid { get; private set; }
protected AObj() { Uid = ++_counter; }
public Comparer Comparer { get; set; }
public int CompareTo(object obj)
{
var other = obj as AObj;
if (other == null) return -1;
return ObjComparer<IObj>.DoCompare(this.Comparer, other.Comparer);
}
}
/// <summary>
/// Thread safe
/// </summary>
public class SortedList2
{
private readonly object _lock = new object();
private int _count;
private readonly Dictionary<Comparer, LinkedList<IObj>> _lookup =
new Dictionary<Comparer, LinkedList<IObj>>();
private readonly SortedSet<Comparer> _set;
private readonly IComparer<Comparer> _comparer;
public SortedList2(IComparer<Comparer> comparer)
{
_comparer = comparer;
_set = new SortedSet<Comparer>(comparer);
}
// O(log n)
public bool Add(IObj i)
{
return this.Add(i, long.MaxValue);
}
// O(log n)
public bool Add(IObj i, long k)
{
lock (_lock)
{
if (i == null || k <= 0) return false;
Comparer val = i.Comparer;
if (_count < k) _count++;
else
{
Comparer max = _set.Max;
if (_comparer.Compare(val, max) >= 0) return false; // Don't add
// Remove old
this.Remove(max);
}
if (_set.Contains(val))
{
_lookup[val].AddLast(i); // Append
}
else
{
// Insert new
_set.Add(val);
var ps = new LinkedList<IObj>();
ps.AddLast(i);
_lookup.Add(val, ps);
}
return true;
}
}
public void AddAll(List<IObj> objs, bool randomizeFirst = false)
{
AddAll(objs, int.MaxValue, randomizeFirst);
}
public void AddAll(List<IObj> objs, int k, bool randomizeFirst = false)
{
if (randomizeFirst)
{
var list = objs;
#region maintain input order
//list = new List<IObj>();
//list.AddRange(objs);
#endregion
Randomize(list);
foreach (var i in list) Add(i, k);
}
else foreach (var i in objs) Add(i, k);
}
// http://en.wikipedia.org/wiki/Fisher%E2%80%93Yates_shuffle
private static void Randomize(IList<IObj> list)
{
var rand = new Random();
var n = list.Count;
for (var i = 0; i < n; i++)
{
var j = rand.Next(n);
var tmp = list[i];
list[i] = list[j];
list[j] = tmp;
}
}
// O(n)
public List<IObj> GetAll()
{
lock (_lock)
{
var all = new List<IObj>();
var dists = _set.ToList();
foreach (var dist in dists) all.AddRange(_lookup[dist]);
return all;
}
}
public int Count
{
get
{
lock (_lock) return _count;
}
}
// O(log n)
public bool Remove(IObj i)
{
lock (_lock)
{
if (i == null) return false;
var isRemoved = this.Remove(i.Comparer);
if (isRemoved) _count--;
return isRemoved;
}
}
// O(log n)
public bool Remove(Comparer val)
{
lock (_lock)
{
return this.RemoveHelper(val);
}
}
// O(log n)
private bool RemoveHelper(Comparer val)
{
if (_set.Contains(val))
{
var bag = _lookup[val];
bag.RemoveLast(); // O(1)
if (bag.Count == 0)
{
_lookup.Remove(val); // O(1)
_set.Remove(val); // O(log n)
}
return true;
}
return false;
}
}
public class ObjComparer<T> : IComparer<T> where T : IComparable
{
public int Compare(T a, T b)
{
return DoCompare(a, b);
}
public static int DoCompare<U>(U a, U b) where U : IComparable
{
return a.CompareTo(b); // ascending
//return b.CompareTo(a); // descending
}
}
// http://en.wikipedia.org/wiki/Selection_algorithm
public class Selection
{
public List<IObj> List = new List<IObj>();
public int K = 1;
public List<IObj> GetAll()
{
return List.Take(K).ToList();
}
/*
function select(list[1..n], k)
for i from 1 to k
minIndex = i
minValue = list[i]
for j from i+1 to n
if list[j] < minValue
minIndex = j
minValue = list[j]
swap list[i] and list[minIndex]
return list[k]
*/
public void Algo()
{
var n = List.Count;
for (int i = 0; i < K; i++)
{
var minIndex = i;
var minValue = List[i];
for (int j = i + 1; j < n; j++)
{
if (List[j].CompareTo(minValue) < 0)
{
minIndex = j;
minValue = List[j];
}
}
Swap(i, minIndex);
}
}
void Swap(int i, int j)
{
var tmp = List[i];
List[i] = List[j];
List[j] = tmp;
}
}
}
Facebook Hacker Cup 2013 Round 1 Solution part 1
Card Game
References:
FB hacker cup
Analysis
John is playing a game with his friends. The game’s rules are as follows: There is deck of N cards from which each person is dealt a hand of K cards. Each card has an integer value representing its strength. A hand’s strength is determined by the value of the highest card in the hand. The person with the strongest hand wins the round. Bets are placed before each player reveals the strength of their hand.
John needs your help to decide when to bet. He decides he wants to bet when the strength of his hand is higher than the average hand strength. Hence John wants to calculate the average strength of ALL possible sets of hands. John is very good at division, but he needs your help in calculating the sum of the strengths of all possible hands.
Problem
You are given an array a with N ≤ 10 000 different integer numbers and a number, K, where 1 ≤ K ≤ N. For all possible subsets of a of size K find the sum of their maximal elements modulo 1 000 000 007.
Input
The first line contains the number of test cases T, where 1 ≤ T ≤ 25
Each case begins with a line containing integers N and K. The next line contains N space-separated numbers 0 ≤ a [i] ≤ 2 000 000 000, which describe the array a.
Output
For test case i, numbered from 1 to T, output “Case #i: “, followed by a single integer, the sum of maximal elements for all subsets of size K modulo 1 000 000 007.
Example
For a = [3, 6, 2, 8] and N = 4 and K = 3, the maximal numbers among all triples are 6, 8, 8, 8 and the sum is 30.
Example input
5
4 3
3 6 2 8
5 2
10 20 30 40 50
6 4
0 1 2 3 5 8
2 2
1069 1122
10 5
10386 10257 10432 10087 10381 10035 10167 10206 10347 10088
Example output
Case #1: 30
Case #2: 400
Case #3: 103
Case #4: 1122
Case #5: 2621483
Solution by Facebook
reference:
The was the simplest problem in the competition with a 60% of success rate.
For a given an array a of n distinct integers,
we need to print the sum of maximum values among all possible subsets with k elements.
The final number should be computed modulo MOD=1000000007, which is a prime number.
First we should sort all numbers, such that a [1] < a [2] < ... < a [n].
Let's see in how many times the number a [i] appears as the maximum number in some subsets,
provided that i >= k. From all numbers less than a [i] we can choose any k - 1,
which is exactly equal to bin [i - 1][k - 1] where bin [n][k] is a binomial coefficient
(see http://en.wikipedia.org/wiki/Binomial_coefficient).
Therefore, the final solution is the sum of a [i] * bin [i - 1][k - 1],
where i goes from k to n, and we need to compute all binomial coefficients
bin [k - 1][k - 1], ..., bin [n - 1][k - 1].
That can be done in many ways.
The simplest way is to precompute all binomial coefficient using simple recurrent formula
bin [0][0] = 1;
for (n = 1; n < MAXN; n++) {
bin [n][0] = 1;
bin [n][n] = 1;
for (k = 1; k < n; k++) {
bin [n][k] = bin [n - 1][k] + bin [n - 1][k - 1];
if (bin [n][k] >= MOD) {
bin [n][k] -= MOD;
}
}
}
qsort (a, n, sizeof(long), compare);
sol = 0;
for (int i = k - 1; i < n; i++) {
sol += ((long long) (a [i] % MOD)) * bin [i][k - 1];
sol = sol % MOD;
}
Note that we are not using % operator in the calculation of the binomial coefficient,
as subtraction is much faster.
The overall time complexity is O (n log n) for sorting and O (n^2)
for computing the binomial coefficients.
Another way is to use recurrent formula
bin [n + 1][k] = ((n + 1) / (n + 1 - k)) * bin [n][k]
and use Big Integer arithmetics involving division. As this might be too slow,
these values can be precomputed modulo MOD and stored in a temporary file
as the table is independent of the actual input and thus needs to be computed only once.
Since MOD is a prime number and use calculate the inverse of the number (n + 1 - k)
using Extended Eucledian algorithm (see http://en.wikipedia.org/wiki/Modular_multiplicative_inverse)
and multiply with the inverse instead of dividing. This yields on O(n log n) solution.
By direct definition bin [n][k] = n! / (n - k)! k!, one can iterate through all prime numbers p
less than or equal to n, and calculate the power of p in bin [n][k] using the formula
a (n, k) = [n / p] + [n / p^2] + [n / p^3] + ... for the maximum power of p dividing the factorial n!.
The most common mistakes were because competitors did not test the edge cases
when k = 1 or k = n, and forgot to define bin [0][0] = 1.
Another mistake was not storing the result in a 64-bit integer when multiplying two numbers.
Program.cs
using System;
using System.Collections.Generic;
using System.Diagnostics;
using System.IO;
using System.Linq;
/// <summary>
/// Author: Kunuk Nykjaer
/// </summary>
class Program
{
static void Main(string[] args)
{
var sw = new Stopwatch();
sw.Start();
var lines = ReadFile("input.txt");
Run(lines.ToList());
sw.Stop();
Console.WriteLine("Elapsed: {0}", sw.Elapsed.ToString());
Console.WriteLine("press exit.. ");
Console.ReadKey();
}
static void Run(IList<string> lines)
{
var result = new List<string>();
var nb = 1;
for (var i = 1; i < lines.Count; i += 2)
{
if (string.IsNullOrWhiteSpace(lines[i])) continue;
if (lines[i].StartsWith("#")) continue;
var one = lines[i].Split(new[] { " " }, StringSplitOptions.RemoveEmptyEntries);
var two = lines[i + 1].Split(new[] { " " }, StringSplitOptions.RemoveEmptyEntries);
var n = int.Parse(one[0]);
var k = int.Parse(one[1]);
var numbers = two.Select(int.Parse).ToList();
numbers = numbers.OrderByDescending(x => x).ToList();
var r = Algo(k, numbers);
result.Add(string.Format("Case #{0}: {1}", nb++, r));
}
WriteFile(result);
}
static class Binomial
{
public static long C(long n, long k)
{
// n! / (k! * (n-k)!)
if (n < k) return 0;
if (k == 0 || n == 1) return 1;
if (n == k) return 1;
// This function is less efficient, but is more likely to not overflow when N and K are large.
// Taken from: http://blog.plover.com/math/choose.html
//
long r = 1;
long d;
if (k > n) return 0;
for (d = 1; d <= k; d++)
{
r *= n--;
r /= d;
}
return r;
}
}
static long Algo(int k, IList<int> numbers)
{
const long modulus = 1000000007;
long sum = 0;
for (var i = 0; i < numbers.Count - 1; i++)
{
long a = numbers[i];
var b = Binomial.C(numbers.Count - 1 - i, k - 1);
sum = (sum + ((a * b) % modulus)) % modulus;
}
sum = sum % modulus;
return sum;
}
#region ** File
static IEnumerable<string> ReadFile(string path)
{
var list = new List<string>();
try
{
using (var reader = new StreamReader(path, true))
{
var line = reader.ReadLine();
while (line != null)
{
list.Add(line);
line = reader.ReadLine();
}
}
}
catch { throw; }
return list.ToArray();
}
static bool WriteFile(IEnumerable<string> lines)
{
var fileInfo = new FileInfo("output.txt");
try
{
using (StreamWriter sw = fileInfo.CreateText())
{
foreach (var line in lines) sw.WriteLine(line);
}
return true;
}
catch { throw; }
}
#endregion File
}
Facebook Hacker Cup 2013 Qualification Round Solution part 3
Find the Min
References:
FB hacker cup
Analysis
Solution part 1
Solution part 2
After sending smileys, John decided to play with arrays. Did you know that hackers enjoy playing with arrays? John has a zero-based index array, m, which contains n non-negative integers. However, only the first k values of the array are known to him, and he wants to figure out the rest.
John knows the following: for each index i, where k <= i < n, m[i] is the minimum non-negative integer which is *not* contained in the previous *k* values of m.
For example, if k = 3, n = 4 and the known values of m are [2, 3, 0], he can figure out that m[3] = 1.
John is very busy making the world more open and connected, as such, he doesn't have time to figure out the rest of the array. It is your task to help him.
Given the first k values of m, calculate the nth value of this array. (i.e. m[n – 1]).
Because the values of n and k can be very large, we use a pseudo-random number generator to calculate the first k values of m. Given positive integers a, b, c and r, the known values of m can be calculated as follows:
m[0] = a
m[i] = (b * m[i - 1] + c) % r, 0 < i < k
Input
The first line contains an integer T (T <= 20), the number of test cases.
This is followed by T test cases, consisting of 2 lines each.
The first line of each test case contains 2 space separated integers, n, k
(1 <= k <= 105, k < n <= 109).
The second line of each test case contains 4 space separated integers a, b, c, r
(0 <= a, b, c <= 109, 1 <= r <= 109).
Output
For each test case, output a single line containing the case number and the nth element of m.
Example input
5
97 39
34 37 656 97
186 75
68 16 539 186
137 49
48 17 461 137
98 59
6 30 524 98
46 18
7 11 9 46
Example output
Case #1: 8
Case #2: 38
Case #3: 41
Case #4: 40
Case #5: 12
Program.cs
using System;
using System.Collections.Generic;
using System.Diagnostics;
using System.Globalization;
using System.IO;
using System.Linq;
using System.Text;
using System.Threading;
// C# .Net 4
namespace ConsoleApplicationFB
{
/// <summary>
/// Author: Kunuk Nykjaer
/// Find the Min
/// </summary>
class Program
{
const int MaxK = 100000;
const int MaxN = 1000000000;
private static void Main(string[] args)
{
Thread.CurrentThread.CurrentCulture = CultureInfo.GetCultureInfo("en-US");
var sw = new Stopwatch();
sw.Start();
var lines = ReadFile("input.txt");
Run(lines.ToList());
sw.Stop();
Console.WriteLine("Elapsed: {0}", sw.Elapsed.ToString());
Console.WriteLine("press exit a key to exit ...");
Console.ReadKey();
}
private static void Run(List<string> lines)
{
var result = new List<string>();
var nb = 1;
for (var i = 1; i < lines.Count; i += 2)
{
if (string.IsNullOrWhiteSpace(lines[i])) continue;
if (lines[i].StartsWith("#")) continue;
var one = lines[i].Split(new[] { " " }, StringSplitOptions.RemoveEmptyEntries);
var two = lines[i + 1].Split(new[] { " " }, StringSplitOptions.RemoveEmptyEntries);
var n = int.Parse(one[0]);
var k = int.Parse(one[1]);
var a = int.Parse(two[0]);
var b = int.Parse(two[1]);
var c = int.Parse(two[2]);
var r = int.Parse(two[3]);
var data = new Data { n = n, k = k, a = a, b = b, c = c, r = r };
data.Validate();
data.Populate();
var nth = Algo(data, Debug);
data.Clear();
result.Add(string.Format("Case #{0}: {1}", nb++, nth));
}
WriteFile(result);
}
private static string Algo(Data d, Action<object> debug)
{
debug(string.Format("\nNumber {0}", d.Id));
var sw = new Stopwatch();
sw.Start();
var arr = d.Subset(0, d.k);
var window = new Window();
window.AddRange(arr);
var set = new HashSet<int>();
foreach (var i in arr) set.Add(i);
var candidates = GetCandidates(d, set);
var min = candidates.Min;
candidates.Remove(candidates.Min);
d.m[d.k] = min;
var nk = d.n - d.k;
sw.Stop();
debug("init: " + sw.Elapsed.ToString());
sw.Reset(); sw.Start();
// O(k)
for (var i = 1; i < nk; i++)
{
if (nk > 2 * d.k && i > d.k) // O(1)
{
// Here we cut the running time.
// we know k values are repeating from here
// window only contains values from 0 .. k
// we know the end value will be a value between 0..k
// with clever modulus usage we know the right one
var index = ((nk - 1) % d.k) + d.k - 1;
if (d.k == 1) index += 1; // off by one issue, must be next 'window' in array
var res = d.m[index];
sw.Stop();
debug("Done: " + sw.Elapsed.ToString());
return res.ToString();
}
//O(log k)
var next = min; // update //O(1)
var prev = d.m[i - 1]; //O(1)
window.Remove(prev); //O(1)
window.Add(next); //O(1)
if (!window.Contains(prev)) //O(1)
{
candidates.Add(prev); //O(log k)
}
if (candidates.Count == 0) //O(1)
{
throw new ApplicationException("algo error");
}
min = candidates.Min; //O(log k)
candidates.Remove(candidates.Min); //O(log k)
d.m[i + d.k] = min; //O(1)
}
sw.Stop();
debug("Done: " + sw.Elapsed.ToString());
return d.m[d.n - 1].ToString();
}
// Candidates are numbers from 0 .. K, exlusive already in k first items
static SortedSet<int> GetCandidates(Data data, HashSet<int> set)
{
var candidates = new SortedSet<int>();
for (var i = 0; i <= data.k; i++)
{
if (!set.Contains(i)) candidates.Add(i);
}
return candidates;
}
static void Debug(object o)
{
//Console.WriteLine(o);
}
#region ** Class
class Window
{
readonly Dictionary<int, int> _dict = new Dictionary<int, int>();
public bool Contains(int i)
{
if (_dict.ContainsKey(i)) return _dict[i] > 0;
return false;
}
public void Remove(int i)
{
if (!_dict.ContainsKey(i)) return;
var v = _dict[i];
if (v <= 1) _dict.Remove(i);
else _dict[i]--;
}
public void Add(int i)
{
if (!_dict.ContainsKey(i)) _dict.Add(i, 1);
else _dict[i]++;
}
public void AddRange(IEnumerable<int> list)
{
foreach (var i in list)
{
Add(i);
}
}
}
class Data
{
private static int _count;
public int Id { get; private set; }
public Data() { Id = ++_count; }
public int n;
public int k;
public int a;
public int b;
public int c;
public int r;
public int[] m;
public override string ToString()
{
return string.Format("{0},{1},{2},{3},{4},{5}", n, k, a, b, c, r);
}
public string M()
{
return m.Aggregate("[", (i, j) => i + j + ",") + "]";
}
public void Populate()
{
m = new int[k * 3]; // at least > k * 2
m[0] = a;
for (var i = 1; i < k; i++) Mi(i);
}
void Mi(int i)
{
// m[i] = (b * m[i - 1] + c) % r, 0 < i < k
var ii = (int) ((((long)b * m[i - 1]) + c) % r);
if (ii < 0) throw new ApplicationException("overflow");
m[i] = ii;
}
public void Clear()
{
m = null;
}
public int[] Subset(int i, int j)
{
var arr = new int[j - i];
for (var ii = 0; i < j; i++, ii++) arr[ii] = m[i];
return arr;
}
public void Validate()
{
if (k < 0 || n < 0 || k >= n || k > MaxK || n > MaxN)
{
throw new ApplicationException("invalid params");
}
}
}
#endregion Class
#region ** File
static IEnumerable<string> ReadFile(string path)
{
var list = new List<string>();
try
{
using (var reader = new StreamReader(path, true))
{
var line = reader.ReadLine();
while (line != null)
{
list.Add(line);
line = reader.ReadLine();
}
}
}
catch { throw; }
return list.ToArray();
}
static bool WriteFile(IEnumerable<string> lines)
{
var fileInfo = new FileInfo("output.txt");
try
{
using (StreamWriter sw = fileInfo.CreateText())
{
foreach (var line in lines) sw.WriteLine(line);
}
return true;
}
catch { throw; }
}
#endregion File
}
}
input.txt
20 497151700 96511 9 7 6 999919625 98 59 6 30 524 98 112 73 1 5 3 64100 198 81 8 5 7 83495 46 18 7 11 9 46 137 49 48 17 461 137 131 74 1 9 10 78736 28 21 6 5 1 85919 840698758 13331 8 7 10 999955808 1000000000 100000 99999 1 99999 100000 73 26 5 8 4 54214 110 53 7 7 1 64417 1000000000 100000 1 1 0 2 1000000000 1 12 7 74 12 1000000000 100000 1 1 1 1000000000 45068754 29153 2 9 5 999904402 1000000000 100000 999999999 1 999999999 1000000000 59 26 14 19 681 59 249718282 93729 1 5 6 999917908 254 99 1 8 9 74990
Running time: 2 sec.
Facebook Hacker Cup 2013 Qualification Round Solution part 2
Balanced Smileys
References:
FB hacker cup
Analysis
Solution part 1
Solution part 3
Your friend John uses a lot of emoticons when you talk to him on Messenger. In addition to being a person who likes to express himself through emoticons, he hates unbalanced parenthesis so much that it makes him go :(
Sometimes he puts emoticons within parentheses, and you find it hard to tell if a parenthesis really is a parenthesis or part of an emoticon.
A message has balanced parentheses if it consists of one of the following:
– An empty string “”
– One or more of the following characters: ‘a’ to ‘z’, ‘ ‘ (a space) or ‘:’ (a colon)
– An open parenthesis ‘(‘, followed by a message with balanced parentheses, followed by a close parenthesis ‘)’.
– A message with balanced parentheses followed by another message with balanced parentheses.
– A smiley face “:)” or a frowny face “:(”
Write a program that determines if there is a way to interpret his message while leaving the parentheses balanced.
Input
The first line of the input contains a number T (1 ≤ T ≤ 50), the number of test cases.
The following T lines each contain a message of length s that you got from John.
Output
For each of the test cases numbered in order from 1 to T, output “Case #i: ” followed by a string stating whether or not it is possible that the message had balanced parentheses. If it is, the string should be “YES”, else it should be “NO” (all quotes for clarity only)
Constraints
1 ≤ length of s ≤ 100
Example input
5
:((
i am sick today (:()
(:)
hacker cup: started :):)
)(
Example output
Case #1: NO
Case #2: YES
Case #3: YES
Case #4: YES
Case #5: NO
Program.cs
using System;
using System.Collections.Generic;
using System.IO;
using System.Linq;
// C# .Net 4
namespace ConsoleApplicationFB
{
/// <summary>
/// Author: Kunuk Nykjaer
/// Balanced Smileys
/// </summary>
class Program
{
const char Beg = '(';
const char End = ')';
const char Colon = ':';
static void Main(string[] args)
{
var lines = ReadFile("input.txt");
Run(lines);
}
static void Run(IList<string> lines)
{
var result = new List<string>();
for (var i = 1; i < lines.Count; i++)
{
var value = Algo(lines[i]) ? "YES" : "NO";
result.Add(string.Format("Case #{0}: {1}", i, value));
}
WriteFile(result);
}
static bool Algo(string line)
{
if (string.IsNullOrWhiteSpace(line)) return true;
var result = new List<Path>();
// Recursive version, simpler imple, but will stackoverflow on large dataset
Recursive(new Path { Line = line }, result);
// Stack version, less simpler imple, but handles large dataset better
//Loop(new Path { Line = line }, result);
return result.Any(i => i.Valid);
}
// Recursive version
static void Recursive(Path p, List<Path> result)
{
if (result.Count > 0) return; // found a valid path, don't eval others
for (var i = 0; i < p.Line.Length; i++)
{
var c = p.Line[i];
if (c == Colon)
{
if (i + 1 < p.Line.Length)
{
var c2 = p.Line[i + 1];
if (IsParan(c2))
{
// split path to smiley and parantheses
var smiley = p.Line.Substring(i + 2);
var paran = p.Line.Substring(i + 1);
// Eval smiley path first
Recursive(new Path
{
Line = smiley,
Stack = p.Stack
},
result);
Recursive(new Path
{
Line = paran,
Stack = p.Stack
},
result);
return; // end current branch
}
}
}
else if (c == Beg) p.Stack++;
else if (c == End)
{
if (p.Stack == 0) return; // Invalid path
p.Stack--;
}
else if (IsText(c)) { } // Valid
else return; // Invalid path
}
if (p.Stack != 0) return;
// Found valid path
p.Valid = true;
result.Add(p);
}
// Stack version
static void Loop(Path path, List<Path> result)
{
// Stop on first found valid path
var stack = new Stack<Path>();
stack.Push(path);
#region while
while (stack.Count > 0)
{
var p = stack.Pop();
var endbranch = false;
# region loop
for (var i = 0; i < p.Line.Length; i++)
{
var c = p.Line[i];
if (c == Colon)
{
if (i + 1 < p.Line.Length)
{
var c2 = p.Line[i + 1];
if (IsParan(c2))
{
// Split path to smiley and parantheses
var smiley = p.Line.Substring(i + 2);
var paran = p.Line.Substring(i + 1);
stack.Push(new Path
{
Line = paran,
Stack = p.Stack
});
// Always eval smiley paths first, push last
stack.Push(new Path
{
Line = smiley,
Stack = p.Stack
});
endbranch = true;
}
}
}
else if (c == Beg) p.Stack++;
else if (c == End)
{
p.Stack--;
if (p.Stack < 0) endbranch = true; // Invalid path
}
else
{
if (IsText(c)) {} // Valid
else endbranch = true; // Invalid path
}
if (endbranch) break;
}
// Done branch
if (endbranch) continue; // Eval next stack
if (p.Stack != 0) continue; // Eval next stack
// Found valid path
p.Valid = true;
result.Add(p);
return; // Don't evaluate other branch, we have a valid path
#endregion loop
}
#endregion while
}
static bool IsParan(char c)
{
return c == Beg || c == End;
}
static bool IsText(char c)
{
const int a = (int)'a';
const int z = (int)'z';
if (c == ' ') return true;
if (c == Colon) throw new ApplicationException("algo error");
if (c >= a && c <= z) return true;
return false;
}
class Path
{
public string Line = "";
public int Stack = 0;
private static int _counter = 0;
private int Id { get; set; }
public Path() { Id = ++_counter; }
public bool Valid = false;
public override string ToString()
{
return string.Format("{0}; {1}; {2}; {3}", Id, Stack, Valid, Line);
}
}
#region File
static IList<string> ReadFile(string path)
{
var list = new List<string>();
try
{
using (var reader = new StreamReader(path, true))
{
var line = reader.ReadLine();
while (line != null)
{
list.Add(line);
line = reader.ReadLine();
}
}
}
catch { throw; }
return list.ToArray();
}
static bool WriteFile(IEnumerable<string> lines)
{
var fileInfo = new FileInfo("output.txt");
try
{
using (StreamWriter sw = fileInfo.CreateText())
{
foreach (var line in lines) sw.WriteLine(line);
}
return true;
}
catch { throw; }
}
#endregion File
}
}
Running time: 1 sec.
input.txt
20 (:) :((:()):))(a::(:)))(aa)a(a)()():)a(()(::()))((((()a)a((((()())((a()()()(()()(():a))()a)):a)))))) hacker cup: started :):) a()(())(())(:)(:((:aa)()(a(():()()a)a()():(((:))()(()(a:(:aa)())))(:::()((::aa)))))(:)(((()()) )( i am sick today (:() (:)())()a()(()::(():())(:))):((:(a:())()()a)((()(a))()(:a()a:((:)a(())(:)(()())))())(a)))() (:a)) (()()((((((((:)aa())a():(:()a(a)):)()(:))())(a)a((((a:()(a((()()a)a)):(a(a)))a)((():))):a()) ()((:a(a()()a))())((:a(:a)(()a((((a((a(()(:aa()()()))):)(():):)(:(a))():(())(():()):):(()a)) (()a:::)a((:))(::a((a)(::aa((a):(:)(:)a()a(()))))facebook is hiring:)()()()a(a((:(a((:)()()))a)) ()aa():):(a:))a()a(:))()()((()(:((())a)()(:)()):)::(()a:(:(:)((:(:a):(()(((a(())a:aaaa(())))) (:a()a)(a)a(aa(()(::)())(:a(a):()a(a()a(()():)))this is a min cost max flow problem(a)((a(()a)))a :)()((a)):(():a:a:)(:a)):)(()(:)::::(a(::a())(a):(:((((:(aa(()))a)(((((((((()a()a):)))((:))))))))) aa:a:((a)(aa(::((((::((())aaa(()a(()a)))::a(((:(():()aa))a((:a:(:()((:(:():)))()):a(()a(())) ()(((a)((aa)))a)a()(a)(aa:a)()(((:())aa)):()():():a:(a)(a())a:)::a:(aa:):()((a:)())aa)a(a:) :):)(::)a)()a((:a(a(((((a):)))(::()))(a)):))((a))):a:():)):()a(())aa(a(:))(aa()()::)):)(()) :(( (::a((a)a:()):):a)aa:)a(:::))(a())aa(a():))(:)a)((():)(:a:)a))):a(a)((:()(()())a))()a((()a)) (()aa):a:():((a(():(a()(aa((a()(a)(:)()(a(::))):)(:a::a:()aaa::a):a(((()(:)))(((()a:)a::(())))))
